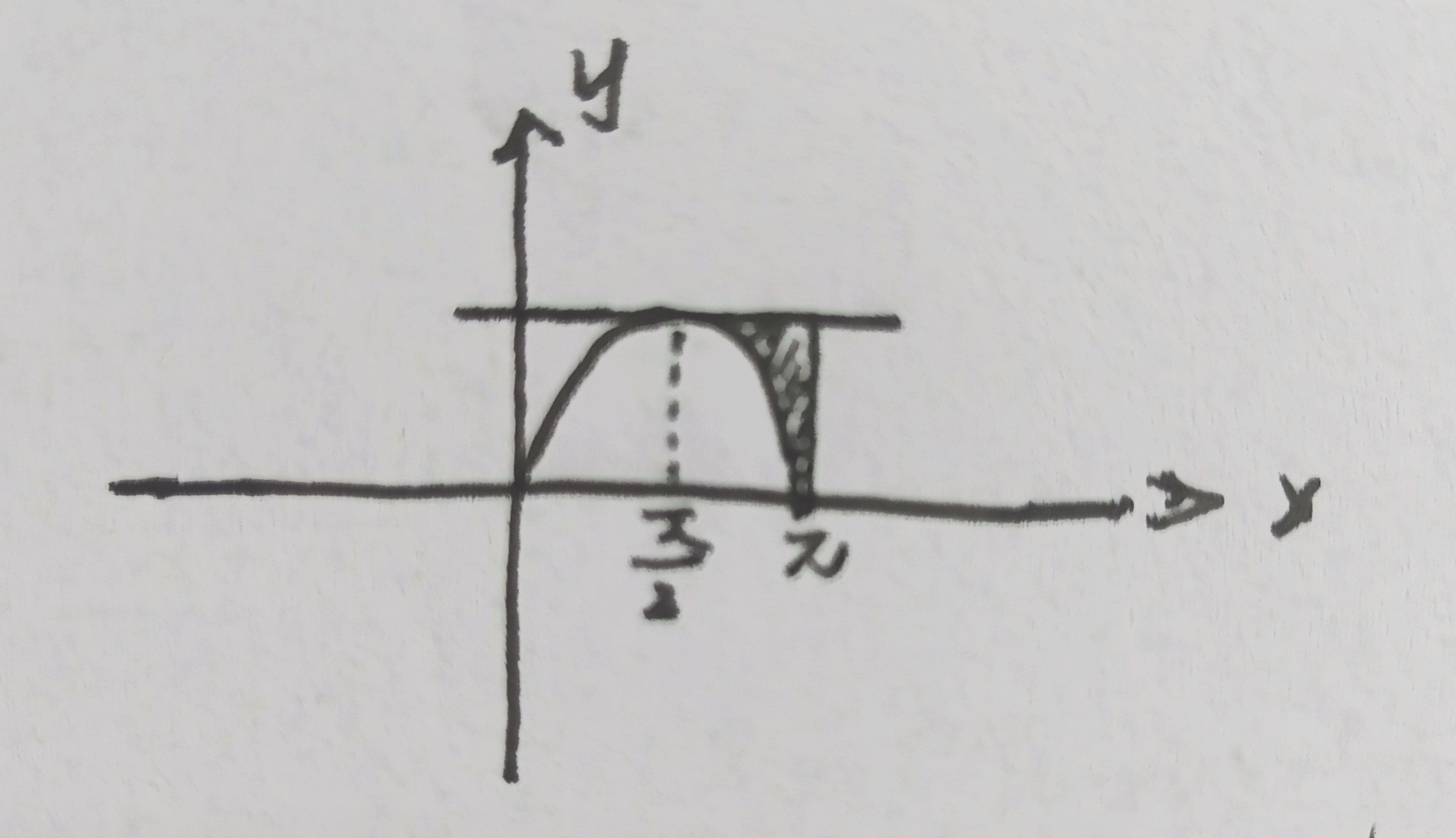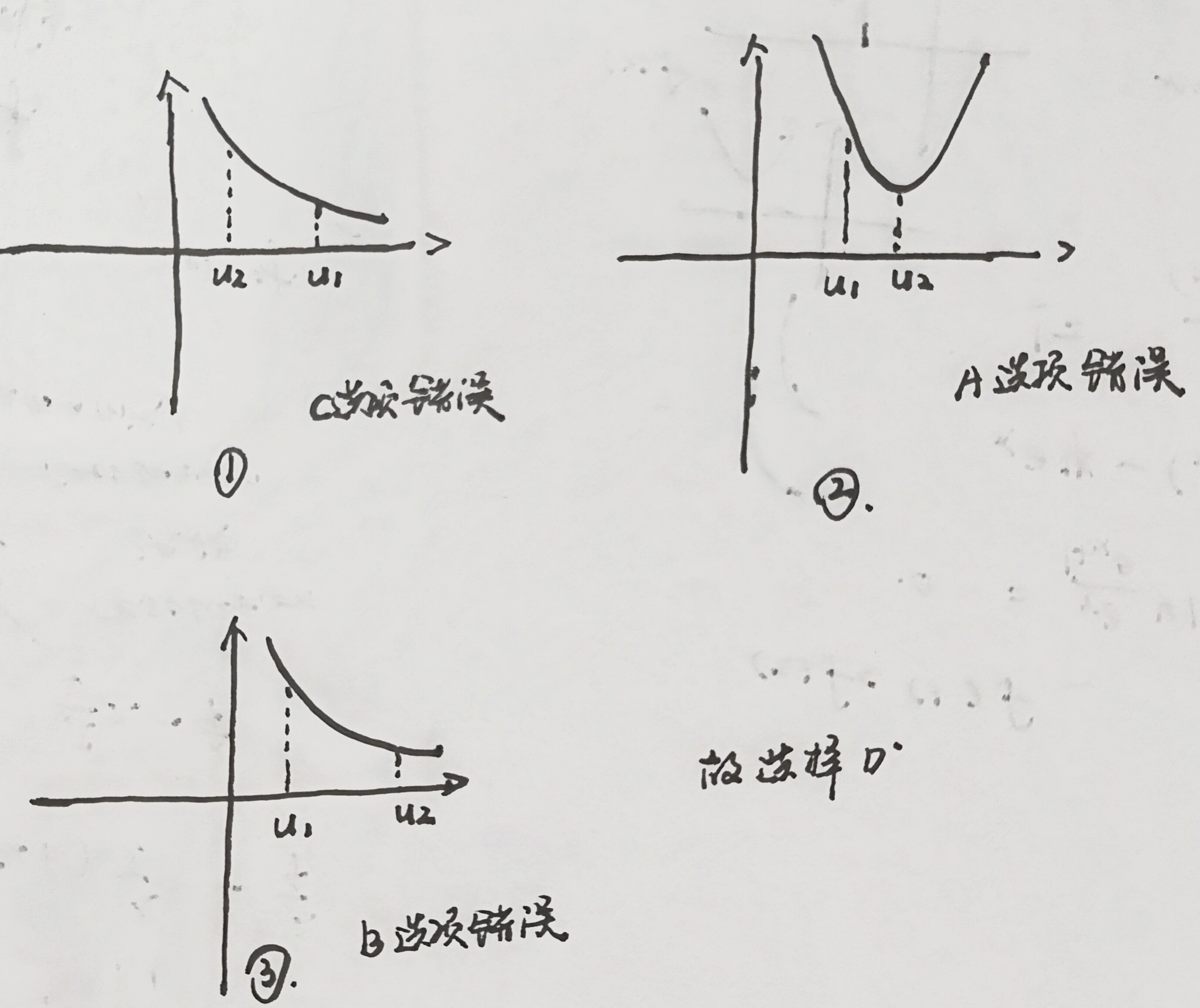
1、设函数 $f(x)$ 在 $(0,\infty)$ 内具有二阶导数，且 $f''(x) > 0$. 令 $u_n=f(n)\,(n=1,2,3...)$，则下列结论正确的是(D)

(A)、若 $u_1>u_2$，则 ${u_n}$ 必收敛

(B)、若 $u_1>u_2$，则 ${u_n}$ 必发散

(C)、若 $u_1<u_2$，则 ${u_n}$ 必收敛

(B)、若 $u_1<u_2$，则 ${u_n}$ 必发散

这道题，是近些年来非常爱考的类型，数列收敛问题，可以采用画图法和反例法，需要熟练理解。

在这里使用画图法进行解决，因为题目中给出了$f''(x) > 0$，所以$f(x)$一定是一个凹函数，根据凹函数的图像性质进行判断则可！

错误的3种情况

---

2、设函数$f(x,y)$连续，则二次积分$\int_{\frac{π}{2}}^πdx\int_{sin\,x}^1f(x,y)dy$等于(B)

(A)、$\int_0^1dy\int_{π+arcsin\,y}^πf(x,y)dx$

(B)、$\int_0^1dy\int_{π-arcsin\,y}^πf(x,y)dx$

(C)、$\int_0^1dy\int_{\frac{π}{2}}^{π+arcsin\,y}f(x,y)dx$

(D)、$\int_0^1dy\int_{\frac{π}{2}}^{π-arcsin\,y}f(x,y)dx$

破题点在于$arcsin\,x$的值域为$[-\frac{π}{2},\frac{π}{2}]$，且只能为这个。

根据题目画出区域D。

区域D

在$x∈[\frac{π}{2},π]$时，$arcsin\,y$的值域也为$[\frac{π}{2},π]$，显然不满足其性质，换句话说$y=sin\,x$的定义域要为$[-\frac{π}{2},\frac{π}{2}]$，因为$y=sin\,x$，根据三角公式可得$y=sin(π-x)$在$x∈[\frac{π}{2},π]$，其定义域就变为了$[0,\frac{π}{2}]$，符合性质！

故选择B

---

3、设函数$f(x),g(x)$在$[a,b]$上连续，在$(a,b)$内具有二阶导数且存在相等的最大值，$f(a)=g(a),f(b)=g(b)$，证明：存在$ξ∈(a,b)$，使得$f''(ξ)=g''(ξ)$.

给出了$f(x),g(x)$在a，b点值的关系，且求证也是关于这两个函数，容易想到构造函数。

令$h(x)=f(x)-g(x)$的话，并能找到$h'(x_1)=h'(x_2)$，则利用罗尔定理，这道题就迎刃而解了，所以重点就是利用题目中的信息，想办法找到两个点使得$h'(x_1)=h'(x_2)$！

利用$f(a)=g(a),f(b)=g(b)$，易得在$h(a)=h(b)=0$。

因为两个函数取得最大值对应的$x_f,x_g$有不同的情况，所以需要讨论。

当$x_f=x_g$时，令$c=x_f$；

当$x_f<x_g$时，有$h(x_f)>0,h(x_g)<0$，故在$(x_f,x_g)$区间内存在一点$x_u$，使得$h(x_u)=0$，令$c=x_u$；

当$x_f>x_g$时，同理

故在$(a,c)$中有一点$x_m$，使得$h'(x_m)=0$，在$(c,b)$中有一点$x_n$，使得$h'(x_n)=0$，由此可得，在$(x_m,x_n)$中存在一点$ξ$，使得$h''(ξ)=0$，既证！

更新日志

2025/7/10 10:41

查看所有更新日志

• d45b4-docs:高数07年真题🚀于 2025/7/10
• 12b62-docs:真题总结🚀于 2025/7/7

版权所有

版权归属：代码・生 活・THINKING

许可证：署名 4.0 国际 (CC-BY-4.0)