• (1).证明：对任意的正整数n，都有$\frac{1}{n+1}<ln\,(1+\frac{1}{n})<\frac{1}{n}$成立.

• (2).设$a_n=1+\frac{1}{2}+...+\frac{1}{n}-ln\,n\,(n=1,2,...)$，证明数列$\{a_n\}$收敛.

第一问利用拉格朗日中值定理，将$ln\,(x+1)-ln\,(x)$展开，可轻易求证.

第二问，求证数列收敛，典型方法就是得到数列单调有界。根据题目可得$a_{n+1}=1+\frac{1}{2}+...+\frac{1}{n+1}-ln\,(n+1)$，用$a_{n+1}$减去$a_n$得： $\frac{1}{n+1}-ln\,(1+\frac{1}{n})<0$，所以数列$\{a_n\}$单调递减，根据题目中的式子，可得：$a_n>ln\,2+ln\,\frac{3}{2}+...+\frac{n+1}{n}-ln\,n$， 消去后，可得$a_n>ln\,(n+1)-ln\,n>0$，所以数列$\{a_n\}$有下界。

即证！

---

2、已知函数$f(x,y)$具有二阶连续偏导数，且$f(1,y)=0,f(x,1)=0,\iint\limits_Df(x,y)\,dxdy=a$，其中$D={(x,y)\,|\,0\le x\le 1,0\le y \le 1}$， 计算二重积分$I=\iint\limits_Dxyf''_{xy}(x,y)\,dxdy$.

因为被积函数中的是二阶导数，而给出的是x=1，关于y的函数和y=1，关于 x的函数，求导后，对应的偏导数在x=1和y=1时，为0.

知道了偏导数为0，被求的又是二阶导数，则不能以常规思路解决这道题，需要将偏导数凑到d之后，想办法凑成$\int_0^1\,dx\int_0^1\,dyf(x,y)\,dxdy=a$.

---

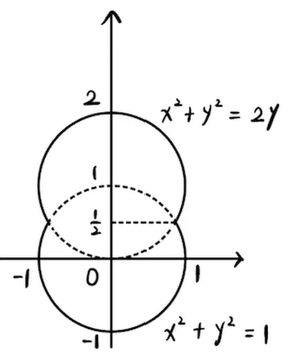
3、一容器的内侧是由图中曲线绕y轴旋转一圈而成的曲面，该曲面由$x^2+y^2=2y(y\ge\frac{1}{2})$与$x^2+y^2=1(y\le\frac{1}{2})$连接而成.

(1).求容器的容积

(2).若将容器内盛满的水从容器顶部全部抽出，至少需要做多少的功？

（长度单位为$m$，重力加速度为$g\,m/s^2$，水的密度为$10^3kg/m^3$）

3、题图

第一题利用武忠祥老师的统一方法解决则可，非常简单，不再赘叙，答案为$\frac{9}{4}π(m^3)$.

第二题利用微元法解决，将整个容积视为一层一层的水层，每层水都需要移动到y=2处（因为是至少的做的功），显然，上部分需要做得功和下部分需要做的功，需要分开计算。

分析下部分，上部分同理。因为做得功为$W=mgh$，展开为$W=pVgh$，其中$V,h$会随着y的变化而变化，得$W_下=\int_{-1}^{\frac{1}{2}}πx_1^2(2-y)dy$.

上部分同理，得$W_上=\int_{\frac{1}{2}}^1πx_2^2(2-y)dy$.两式结果相加，得到$W_总=\frac{27}{8}πgh(J)$.

更新日志

2025/7/16 15:07

查看所有更新日志

• 52b2f-docs:高数-真题-11🚀于 2025/7/16

版权所有

版权归属：代码・生 活・THINKING

许可证：署名 4.0 国际 (CC-BY-4.0)