行列式

约 1785 字大约 6 分钟

2025-06-03

行列式的性质中，行与列的地位相同，为了方便，只说明行，列是一样的！

行列式的几何意义为体积，n阶行列式的值就为在n维空间中行向量构成形状的体积，了解即可，对于做题没啥用。

行列式最基本的定义：每行取一个数，且每行取得数不在同一列，将所有可能性的代数式相加，就得到行列式的值，这里的代数式是在每行取得数相乘的基础上再乘上 “ $-1^{逆序数(行数从小到大，每行元素的列数排列)}$ ”

行列式的性质

行列式转置后值不变
行列式两行互换，值变为相反数
行列式中的某一行加上另一行的k倍，值不变
行列式中某一行的公因数可以提到外部，值不变（注意：一次只能提一行，和矩阵有区别）
行列式可以将一行拆为个数相加，其余行不变，行列式同时也可拆为两个行列式相加，值不变

行列式的展开定理

某行元素与本行代数余子式的乘积之和=行列式的值

某行元素与另一行代数余子式的乘积之和=0（相当于该行列式中有两行元素相同）

常见的行列式结论

$|A^T|=|A|$
$|A^{-1}|=\frac{1}{|A|}$
$|A^*|=|A|^{n-1}$
$|kA|=k^n|A|$
$|A^n|=|A|^n$
$|AB|=|A||B|$

具体行列式的计算

爪形行列式

\begin{vmatrix} x & a_1 & a_2 & \dots & a_n \\ b_1 & y_1 & 0 & \dots & 0 \\ b_2 & 0 & y_2 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_n & 0 & 0 & \dots & y_n \end{vmatrix}

形如上述的行列式，当然，不止这个，斜边和直角边可以不同，但始终都呈现一个“爪”形。

计算方法是用斜边去消除直角边，这样一条直角边上只会有一个非零元素，利用展开定理就可以得到最终结果，较为简单。

异爪形行列式

和爪形的区别在于一条直角边变为较斜边，计算方法有递推法和直角边展开法。

递推法将较斜边和直角边所夹住的直角边按展开定理展开，利用递推求解。

直角边展开法是从构成异爪的直角边展开，展开时可以视为分块矩阵，这样计算代数余子式较为简单。

这里推荐使用递推法！

三对角行列式

D_n = \begin{vmatrix} a & b & 0 & \dots & 0 & 0 \\ c & a & b & \dots & 0 & 0 \\ 0 & c & a & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \dots & a & b \\ 0 & 0 & 0 & \dots & c & a \end{vmatrix}

首先按第一行展开，得到一个递推式，之后可以采用差分方程或者递推法和归纳法进行求解。

展开式是固定的，这里给出结论 $D_n=aD_{n-1}-bcD_{n-2}$ ，得到 $D_n-aD_{n-1}+bcD_{n-2}=0$ .

可以有特征方程 $r^2-ar+bcr=0$ ，解得特征值 $r_1,r_2$ .由此可得 $D_n$ 的表达式：

D_n = \begin{cases} C_1 r_1^n + C_2 r_2^n, & \text{如果 } r_1 \neq r_2 \\ (C_1 + C_2 n) r^n, & \text{如果 } r_1 = r_2 = r \end{cases}

这里的 $C_1,C_2$ 可以通过带入 $D_1,D_2$ 求解出来，相当于求解一个二元一次方程组。

还可以使用递推法进行处理，因为递推法只能处理两个通项的关系，而三对角行列式的递推公式中存在三个通项，所以，首先得凑成两个通项的形式。

设为 $D_n-aD_{n-1}=k(D_{n-1}-aD_{n-2})$ ，将 $D_n-aD_{n-1}$ 视为一个新的通项 ${B_n}$ ，则利用凑出来的递推公式，可以得到 $B_n$ 的式子，再利用 $B_n$ 求出 $D_n$ 则可。

这里推荐使用差分方程，简单，快速，不易出错！

数学归纳法，用于知道结果，反过来证明结果正确的方法，分为第一数学归纳法和第二数学归纳法。前者用于两个通项的递推式，后者用于三个通项的递推式。

一般思路，首先验证需要用到的前几个元素满足递推式，然后设n在小于k时也满足，求出 $D_k=aD_{k-1}-bcD_{k-2}$ ，观察是否满足递推式，满足则成立，否则不成立。

其他行列式

每行各自相加得到一致的结果，将所有列加到同一列上，提出公因数，得到一列1，再用这列1去处理
加边法，这个不是一个必须的方法，但是可以方便消去，左上角补上一列、一行元素，注意一行补充对应元素列上的公共元素

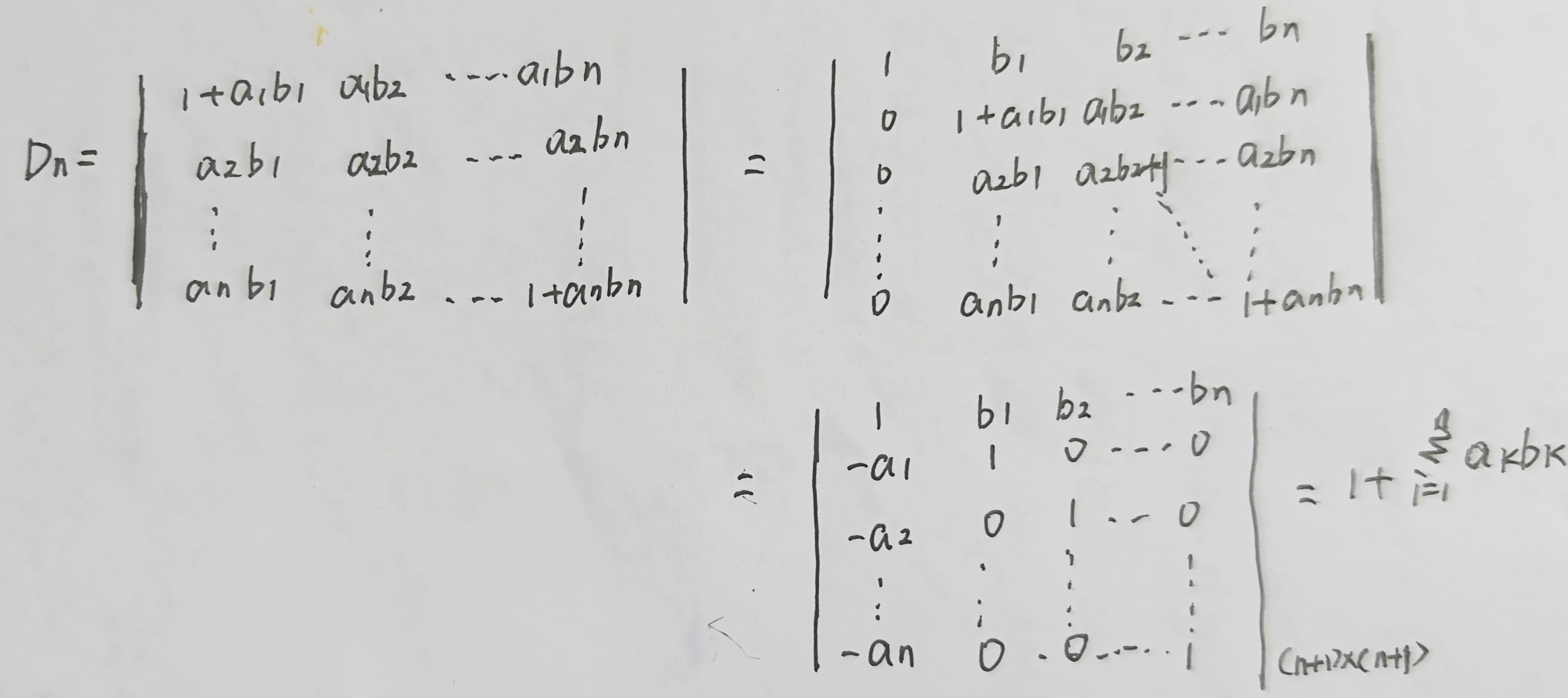
逐行相消，从上到下或从下到上，依次相减。如：第一行减第二行，第二行减第三行，....，第n-1行减第n行
其余的行列式就见招拆招，用一行先消去其他行，尽量将一行中凑出更多的0，这样展开就简单些

抽象行列式

使用行列式性质、矩阵性质和相似理论解决，具体公式在下一节内容中。

代数余子式之和

求某一行线性组合代数余子式之和

若矩阵对应的伴随矩阵好求，可以直接求出，想要什么线性组合代数余子式都可以轻松得到，否则，可以将矩阵的对应行换为线性组合前面对应的系数，求出改变后的行列式值也行。

求线性组合余子式之和

根据余子式和代数余子式的关系，将这个问题转换为上个问题，若行列数相加为奇数，则前面系数需要取负，否则系数不变。

求所有元素对应代数余子式之和

求出矩阵的伴随矩阵，将伴随矩阵中的每个元素相加
求出每行代数余子式，再相加
将行列式|A|每个元素加1，得到新的行列式|B|，用|B|-|A|，为结果

求对角元素对应的代数余子式之和

首先提出一个结论：若给出矩阵 $A$ 的特征值，那么 $A^*$ 的特征值可以快速求解，将 $A$ 的一个特征值不看，剩余的特征值相乘，就为对应 $A^*$ 的一个特征值，以此类推，直到 $A$ 中所有特征值对应的 $A^*$ 特征值都计算完，则可。

因为对角线元素之和为矩阵特征值之和，所以，若题目中给出特征值或可以求出特征值，就可以相加，得到结果。

若题目中矩阵的伴随矩阵好求，也可以将其求解出来，这下想要什么就有什么了。

除了上述的各种经典的方法外，还需要通过练习获得更多的题感。

更新日志

2025/7/20 14:44

查看所有更新日志

74203-docs:高数-行列式🚀于 2025/7/20
bea7a-docs:高数🚀于 2025/7/16
91c07-docs:高数-行列式部分总结🚀于 2025/7/15
19cb2-fix:the project add于 2025/6/21
7b20b-fix:git-balabala🚀于 2025/6/21
f4d02-fix:移动目录🚀于 2025/6/14
561cf-fix:移动目录🚀于 2025/6/14
2d239-fix:重构代码-白色背景🚀于 2025/6/13
57d21-docs:math🚀于 2025/6/3

版权所有

版权归属：代码・生活・THINKING

许可证：署名 4.0 国际 (CC-BY-4.0)

翻译

单词

技巧

作文

高数

线性代数

行列式