代码・生 活・THINKING

外观

矩阵

约 2673 字大约 9 分钟

2025-06-06

矩阵乘法

矩阵相乘，内标值要相同。Am×nBn×s=CmsA_{m×n}B_{n×s}=C_{ms}.

矩阵乘法不满足交换律。AB≠BA,(A+B)2≠A2+2AB+B2,(A+B)(A−B)≠A2−B2AB\neq BA,(A+B)^2\neq A^2+2AB+B^2,(A+B)(A-B)\neq A^2-B^2. 但在某些情况下也可以交换。首先满足的大前提是交换的两个矩阵必须是同阶，然后下面给出各种不同的情况：

  • kE与任何矩阵可交换kE与任何矩阵可交换

  • 两个对角矩阵可交换两个对角矩阵可交换

  • A,A−1,A∗，两两均可交换，A,AT一般不可交换A,A^{-1},A^*，两两均可交换，A,A^T一般不可交换

  • f(A),g(A)可交换f(A),g(A)可交换

  • 若A和B可交换，则AT和BT、A−1和B−1、A∗和B∗、f(A)和g(A)均可交换若A和B可交换，则A^T和B^T、A^{-1}和B^{-1}、A^*和B^*、f(A)和g(A)均可交换

矩阵乘法不满足消去律。AB=0⇏A=0或B=0,AB=AC⇏B=C,AB=CB⇏A=CAB=0\not\Rightarrow A=0或B=0,AB=AC\not\Rightarrow B=C,AB=CB\not\Rightarrow A=C. 但在某些情况下满足消去律，在下面给出成立的情况：

  • 若A列满秩，则AB=0⇒B=0,AB=AC⇒B=C若A列满秩，则AB=0\Rightarrow B=0,AB=AC\Rightarrow B=C.

  • 若B行满秩，则AB=0⇒A=0,AB=CB⇒A=C若B行满秩，则AB=0\Rightarrow A=0,AB=CB\Rightarrow A=C.

矩阵公式汇总

行列式

1.∣A∣=λ1...λn1. |A|=λ_1...λ_n

2.∣kA∣=kn∣A∣2. |kA|=k^n|A|

3.∣AB∣=∣A∣∣B∣3. |AB|=|A||B|

4.∣An∣=∣A∣n4. |A^n|=|A|^n

转置

1.∣AT∣=∣A∣1. |A^T|=|A|

2.(kA)T=kAT2. (kA)^T=kA^T

3.(AT)T=A3. (A^T)^T=A

4.(An)T=(AT)n4. (A^n)^T=(A^T)^n

5.(A+B)T=AT+BT5. (A+B)^T=A^T+B^T

逆

1.∣A−1∣=1∣A∣1. |A^{-1}|=\frac{1}{|A|}

2.(kA)−1=1kA−12. (kA)^{-1}=\frac{1}{k}A^{-1}

3.(A−1)−1=A3. (A^{-1})^{-1}=A

4.(An)−1=(A−1)n4. (A^n)^{-1}=(A^{-1})^n

伴随

1.∣A∗∣=∣A∣n−11. |A^*|=|A|^{n-1}

2.(kA)∗=kn−1A∗2. (kA)^*=k^{n-1}A^*

3.(A∗)∗=∣A∣n−2A3. (A^*)^*=|A|^{n-2}A

4.AA∗=A∗A=∣A∣E4. AA^*=A^*A=|A|E

三大运算

1.(AT)−1=(A−1)T1. (A^T)^{-1}=(A^{-1})^T

2.(AT)∗=(A∗)T2. (A^T)^*=(A^*)^T

3.(A∗)−1=(A−1)∗=A∣A∣3. (A^*)^{-1}=(A^{-1})^*=\frac{A}{|A|}

穿脱原则

1.(ABC)T=CTBTAT1. (ABC)^T=C^TB^TA^T

2.(ABC)−1=C−1B−1A−12. (ABC)^{-1}=C^{-1}B^{-1}A^{-1}

3.(ABC)∗=C∗B∗A∗3. (ABC)^*=C^*B^*A^*

对角阵

1.A=(a1⋱an)(b1⋱bn)=(b1⋱bn)(a1⋱an)1. A = \begin{pmatrix} a_1 & & \\ & \ddots & \\ & & a_n \end{pmatrix} \begin{pmatrix} b_1 & & \\ & \ddots & \\ & & b_n \end{pmatrix} = \begin{pmatrix} b_1 & & \\ & \ddots & \\ & & b_n \end{pmatrix} \begin{pmatrix} a_1 & & \\ & \ddots & \\ & & a_n \end{pmatrix}

可得：A=(a1b1⋱anbn)可得：A=\begin{pmatrix} a_1b_1 & & \\ & \ddots & \\ & & a_nb_n \end{pmatrix}

2.若V=(λ1⋱λn)2. 若V=\begin{pmatrix} λ_1 & & \\ & \ddots & \\ & & λ_n \end{pmatrix}

则∣V∣=λ1...λn则|V|=λ_1...λ_n

φ(V)=(φ(λ1)⋱φ(λn))φ(V)=\begin{pmatrix} φ(λ_1) & & \\ & \ddots & \\ & & φ(λ_n) \end{pmatrix}

Vn=(λ1n⋱λnn)V^n=\begin{pmatrix} λ_1^n & & \\ & \ddots & \\ & & λ_n^n \end{pmatrix}

V−1=(λ1−1⋱λn−1)V^{-1}=\begin{pmatrix} λ_1^{-1} & & \\ & \ddots & \\ & & λ_n^{-1} \end{pmatrix}

分块矩阵

1.∣A∗0B∣=∣A0∗B∣=∣A∣∣B∣1. \begin{vmatrix} A & * \\ 0 & B \end{vmatrix}=\begin{vmatrix} A & 0 \\ * & B \end{vmatrix}=|A||B|

2.∣0AB∗∣=∣∗AB0∣=(−1)mn∣A∣∣B∣2. \begin{vmatrix} 0 & A \\ B & * \end{vmatrix}=\begin{vmatrix} * & A \\ B & 0 \end{vmatrix}=(-1)^{mn}|A||B|

3.(ABCD)T3. \begin{pmatrix} A & B \\ C & D \end{pmatrix}^T

4.(ABCD)−14. \begin{pmatrix} A & B \\ C & D \end{pmatrix}^{-1}

特殊矩阵

对称矩阵

  • A为对称矩阵  ⟺  A=AT (即aij=aji)A为对称矩阵\iff A=A^T\,(即a_{ij}=a_{ji})

  • 若A为对称矩阵，则AT、A−1、A∗、f(A)均为对称矩阵若A为对称矩阵，则A^T、A^{-1}、A^*、f(A)均为对称矩阵

  • 若A和B均为对称矩阵，则A+B为对称矩阵，当且仅当AB=BA时，AB为对称矩阵若A和B均为对称矩阵，则A+B为对称矩阵，当且仅当AB=BA时，AB为对称矩阵

  • ATA、AAT、A+AT天然为对称矩阵A^TA、AA^T、A+A^T天然为对称矩阵

ATA的性质总结A^TA的性质总结

1.ATA为对称矩阵，可正交对角化1. A^TA为对称矩阵，可正交对角化

2.对∀x≠0,xTATAx≥0,λi≥0,∣A∣≥02. 对\forall x\neq 0,x^TA^TAx\ge 0,λ_i\ge 0,|A|\ge 0

3.ATA正定  ⟺  A列满秩3. A^TA正定\iff A列满秩

4.r(ATA)=r(A),ATAx=0与Ax=0同解4. r(A^TA)=r(A),A^TAx=0与Ax=0同解

反对称矩阵

1.A=−AT (即aij=−aji)1. A=-A^T\,(即a_{ij}=-a_{ji})

2.aii=0,λi=0,∣A∣=02. a_{ii}=0,λ_i=0,|A|=0

3.∀α,αTAα=03. \forall α,α^TAα=0

正交矩阵

  • A为正交矩阵  ⟺  A−1=AT  ⟺  AAT=E  ⟺  行（列）向量组为规范正交基A为正交矩阵\iff A^{-1}=A^T\iff AA^T=E\iff行（列）向量组为规范正交基

  • 若A为正交矩阵，则AT,A−1,A∗,±Ak均为正交矩阵若A为正交矩阵，则A^T,A^{-1},A^*,\pm A^k均为正交矩阵

  • 若A和B均为正交矩阵，则AB为正交矩阵若A和B均为正交矩阵，则AB为正交矩阵

  • 正交矩阵的特征值和行列式只可能为1或−1正交矩阵的特征值和行列式只可能为1或-1

  • 设A=(aij)n×n (n≥3).若AT=A∗ (aij=Aij)，则A为零矩阵或A为正交矩阵且∣A∣=1；若AT=−A∗ (aij=−Aij)，则A为零矩阵或A为正交矩阵且∣A∣=−1设A=(a_{ij})_{n×n}\,(n\ge 3).若A^T=A^*\,(a_{ij}=A_{ij})，则A为零矩阵或A为正交矩阵且|A|=1；若A^T=-A^*\,(a_{ij}=-A_{ij})，则A为零矩阵或A为正交矩阵且|A|=-1

秩为 1 的矩阵

  • r(A)=1  ⟺  A的每行（列）成比例  ⟺  存在α=(a1,a2,...,an)T,β=(b1,b2,...,bn)T，使得A=αβTr(A)=1\iff A的每行（列）成比例\iff 存在α=(a_1,a_2,...,a_n)^T,β=(b_1,b_2,...,b_n)^T，使得A=αβ^T

  • tr(A)=βTα=αTβ=(α,β)=∑i=1naibi=ktr(A)=β^Tα=α^Tβ=(α,β)=\sum\limits_{i=1}^na_ib_i=k

  • A2=kA,An=kn−1AA^2=kA,A^n=k^{n-1}A

  • 特征值λ1=λ2=...=λn−1=0,λn=k.λ=k对应的特征向量为α;λ=0对应的特征向量为(−b2,b1,0,...,0)T,(−b3,0,b1,...,0)T,...,(−bn,0,0,...,b1)T (设b1≠0)特征值λ_1=λ_2=...=λ_{n-1}=0,λ_n=k.λ=k对应的特征向量为α;λ=0对应的特征向量为(-b_2,b_1,0,...,0)^T,(-b_3,0,b_1,...,0)^T,...,(-b_n,0,0,...,b_1)^T\,(设b_1\neq 0)

  • A可对角化  ⟺  k≠0A可对角化\iff k\neq 0

  • 若A为实对称矩阵，非零特征值λ=k对应的单位特征向量为a，则A=kaaT若A为实对称矩阵，非零特征值λ=k对应的单位特征向量为a，则A=kaa^T

  • 若Ax=r有解，则A的列向量与r成比例若Ax=r有解，则A的列向量与r成比例

初等矩阵和初等变化

  • 初等变换：互换、倍加、倍乘

  • 初等矩阵：将单位矩阵通过初等变化得到的矩阵

  • 做一次初等行变换等于左乘一个初等（可逆）矩阵，做一次初等列变换等于右乘一个初等（可逆）矩阵。注意左乘看行变，右乘看列变

  • 任一矩阵A可通过初等行变换化为行最简形，等价于存在可逆矩阵P，使PA=行最简型

  • 任一矩阵A可通过初等列变换化为列最简形，等价于存在可逆矩阵Q，使AQ=列最简型

  • 列满秩矩阵A可通过初等行变换化为上面部分为单位矩阵，下面部分为0的矩阵B，等价于存在可逆矩阵P，使PA=B

  • 行满秩矩阵A可通过初等列变换化为左边部分为单位矩阵，右边部分为0的矩阵B，等价于存在可逆矩阵Q，使AQ=B

  • 可逆矩阵A可通过初等行（列、行列同时）变换化为单位矩阵，等价于存在可逆矩阵P、Q，使PA=E、AQ=E、PAQ=E

  • A可逆等价于A可通过初等变换化为E等价于A是初等矩阵的乘积

  • 初等变换的深刻意义：初等变换不改变秩等价于乘以可逆矩阵不改变秩。推广：左乘列满秩不改变秩，右乘行满秩不改变秩

  • 矩阵A、B等价等价于A、B可通过初等变换转换等价于存在可逆矩阵P、Q，使PAQ=B

  • 矩阵A、B行等价等价于A、B可通过初等行变换转化等价于存在可逆矩阵P，使PA=B

  • 矩阵A、B列等价等价于A、B可通过初等列变换转化等价于存在可逆矩阵Q，使AQ=B

  • 三秩相等：非零子式的最高阶数=行向量组无关向量的个数=列向量组无关向量的个数

求矩阵的逆和伴随方法

一个矩阵，若知道了它的逆或伴随，则可以推出另一者，所以求这两者，本质上是求其中一者而已！

求矩阵A的逆，一般有以下方法：

  • 写为[A∣E][A|E]，变换为[E∣A−1][E|A^{-1}]，这样就求得矩阵的逆

  • 若为4阶矩阵的话，可以将其视为分块矩阵进行计算

当然，这种方法是需要容易消为0的情况，更多的不是这样，可以通过求矩阵的伴随矩阵，来间接地求逆矩阵，根据AA∗=∣A∣EAA^*=|A|E.

求矩阵A的伴随，有多种方法：

  • 二阶矩阵，可以根据口诀“主对调，副变号”，快速解决战斗；四阶矩阵，一般可以视为分块矩阵，进行计算，重点是三阶矩阵，在下面的点中说明

  • 定义法，通过伴随矩阵的定义，分别计算对应元素的代数余子和，需要注意的是位置和符号，这种方法不是很好，容易出错

  • 转圈法，将A写4遍，分为两层，每层2个A，将最外层元素去掉，从上到下，依次计算二阶行列式，计算结果横着排，得到的三阶矩阵B就为A的伴随矩阵，这个方法不用管符号之类的干扰信息，只用计算，很容易，推荐使用

转圈法示例

转圈法示例
转圈法示例

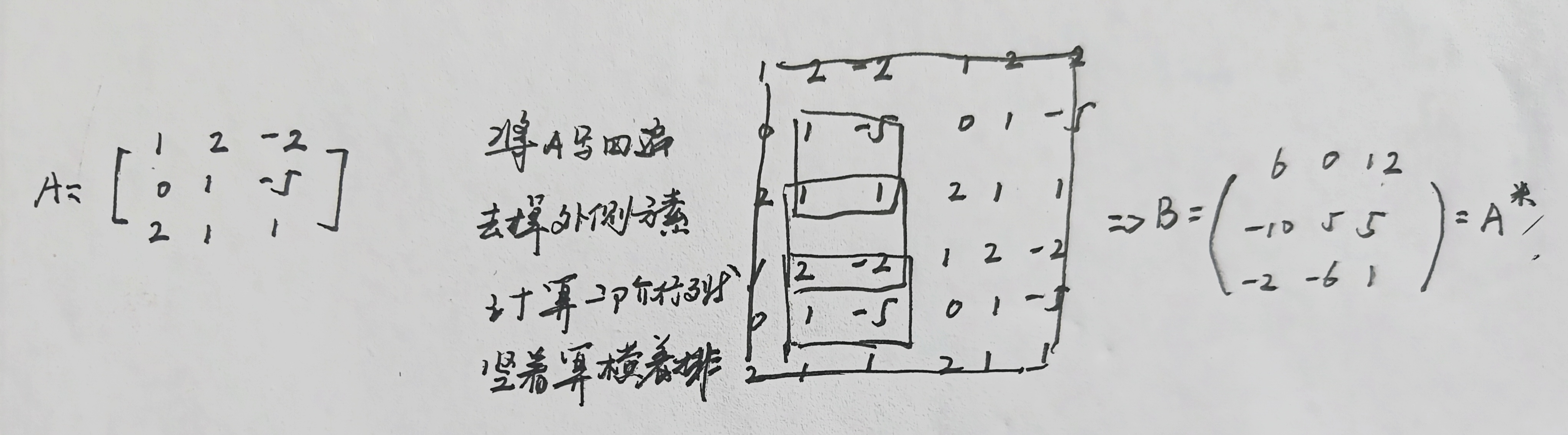
抽象矩阵求逆

可逆矩阵的定义：AB=E、BA=E，则A−1=B；若A为方阵，AB=E，则A−1=B.可逆矩阵的定义：AB=E、BA=E，则A^{-1}=B；若A为方阵，AB=E，则A^{-1}=B.

  • 可逆矩阵×可逆矩阵=可逆矩阵

  • 可逆矩阵×不可逆矩阵=不可逆矩阵

  • 不可逆矩阵×不可逆矩阵=不可逆矩阵

已知r(A)=1r(A)=1，待定系数法求(mA+nE)−1(mA+nE)^{-1}

套路：设(mA+nE)−1=kA+1nE，令(mA+nE)(kA+1nE)=E，求出k则可.设(mA+nE)^{-1}=kA+\frac{1}{n}E，令(mA+nE)(kA+\frac{1}{n}E)=E，求出k则可.

已知矩阵等式，凑因式求逆

题型：

  • 等式仅含有一个矩阵A.已知f(A)=0，求[g(A)]−1.等式仅含有一个矩阵A.已知f(A)=0，求[g(A)]^{-1}.

  • 等式含有一个矩阵A、B.已知f(A,B)=0，求[g(A)]−1.等式含有一个矩阵A、B.已知f(A,B)=0，求[g(A)]^{-1}.

套路：

  • 求矩阵φ(A)，使得φ(A)g(A)=f(A)+kE，幂次从高到低凑出φ(A)，则g(A)−1=1kφ(A).g(A)^{-1}=\frac{1}{k}φ(A).

  • 第二种题型和上述方法一致，不过是凑A、B为f(A,B)而已.

用数的运算类比矩阵运算，恒等变形求逆

题型：求抽象矩阵的逆，但题目未给等式或等式不易化简凑因式。

套路：将矩阵看作一阶矩阵（即一个数），用数的运算进行化简。

数的运算矩阵运算
取倒数:1A取倒数:\frac{1}{A}取逆:A−1取逆:A^{-1}
通分:1A+1B=BAB+AAB通分:\frac{1}{A}+\frac{1}{B}=\frac{B}{AB}+\frac{A}{AB}E的拆分:A−1+B−1=A−1BB−1+A−1AB−1E的拆分:A^{-1}+B^{-1}=A^{-1}BB^{-1}+A^{-1}AB^{-1}

可以通过数的运算快速得到最终答案的形式！便于佐证和排除，同时也提供怎样拆分E的思路。当然，还有种通用的思路，就是遇到逆就提出去，不断地提，就可以得到一个便于计算的式子。

求A的n次幂

只有方阵才可求幂，一般考察二阶或三阶矩阵。

若A为更高阶矩阵，先观察A是否能分块，能分块则先分块再求幂。

归纳法

  • 若r(A)=1，tr(A)=k，则A2=kA,An=kn−1A.A^2=kA,A^n=k^{n-1}A.

  • 若元素较为简单，则试算A2、A3A^2、A^3，找规律.

  • 能用初等变换性质快速得到结果.

A=B+C

若A可拆为两个简单矩阵之和B+C，且B和C可交换，则可将An=(B+C)nA^n=(B+C)^n用二项式定理展开。

一般来说，题目中的矩阵A是拆为B+E的形式，因为这样，利用二项式定理才可以随意的交换，并且会在Bm=0或Bn=BB^m=0或B^n=B，这样才可以化简，不然这样做就没有意义了。

利用相似理论

若题目有给出A~B的提示或A可相似对角化，则可考虑利用相似理论求AnA^n.

若P−1AP=B，则An=(PBP−1)n=PBnP−1.若P^{-1}AP=B，则A^n=(PBP^{-1})^n=PB^nP^{-1}.

若B为对角阵也是一样的，这里主要问题是怎样求其相似和特征值、特征向量。

更新日志

2025/8/19 14:00
查看所有更新日志
  • 9cdc4-docs:每日计划8.19🚀于
  • 76b8c-docs:高数-矩阵-特殊矩阵🚀于
  • 0243c-docs:高数-线代-矩阵🚀于
  • bea7a-docs:高数🚀于
  • 19cb2-fix:the project add于
  • 7b20b-fix:git-balabala🚀于
  • f4d02-fix:移动目录🚀于
  • 561cf-fix:移动目录🚀于
  • 2d239-fix:重构代码-白色背景🚀于
  • b7cbe-docs:holy shit-some fix🚀于

版权归属：代码・生 活・THINKING

许可证：署名 4.0 国际 (CC-BY-4.0)

代码・生 活・THINKING | Copyright © 2023.5.20-至今 阿杰，All rights reserved